PicoCTF 2018 - be-quick-or-be-dead WriteUp

be-quick-or-be-dead are 3 similar reverse challenge.

be-quick-or-be-dead-1

Running the program we see a key “being calculated” After a few seconds of execution, a message says that we need a faster machine and end the process.

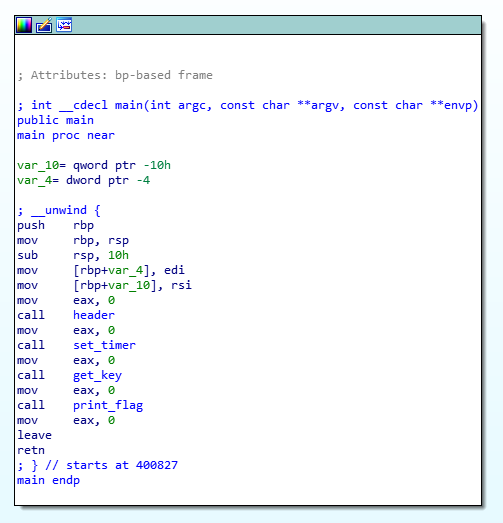
It’s quite simple to see with ida what’s happening

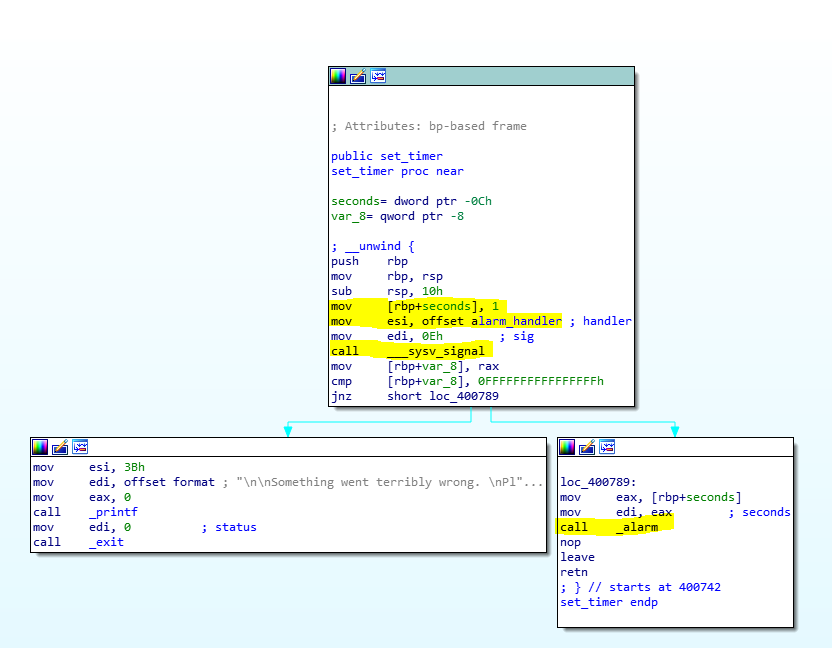
A timer is set, after some time (1 second) it will send a signal to the program to stop the execution, and alarm_handler will be execute

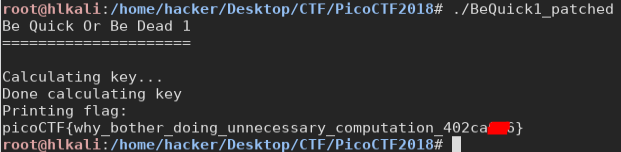
Okay, the first thing we can do is try to give more time before the signal. so, we just patch the “mov [rbp+seconds], 1” into “mov [rbp+seconds], 8” and see what’s happen

Here we are after a few seconds we get the flag!

be-quick-or-be-dead-2

This is very similar, we have the same timer, this time giving us 3 seconds. But the patch applied before isn’t working, (i let it run for more than 5 minutes). In this case, we need to look deeper.

In particular, we should take a look at what makes the program so time-demanding. The main calls a function “get_key” which calls a function “calculate_key”. The return value of calculate_key is moved into eax and will be used later, from the function “decript_key” to decrypt it. So we can’t just skip that.

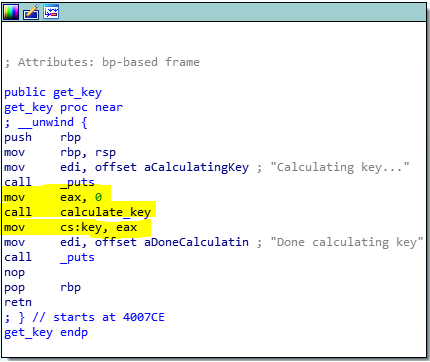
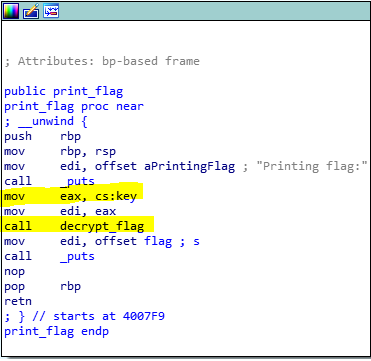
Very good.

So, how this key is generated? Well, calculate_key it’s a one-instruction function it calls fib(3f7h) = fib(1015)

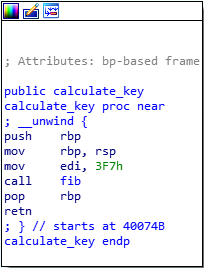
The name should already raise suspicion, but looking at the implementation, it’s clear that it is a recursive version of Fibonacci function.

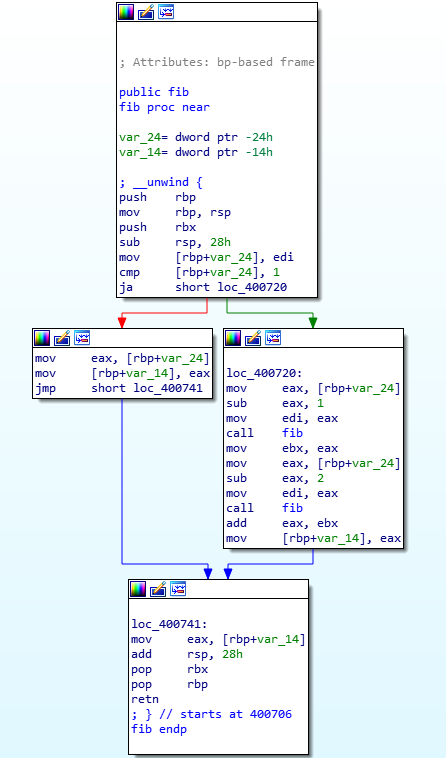
To calculate fib(1015) this isn’t the right way since that implementation has an exponential computational complexity. We could write our function to do it better, or we could ask to WolframAlpha.

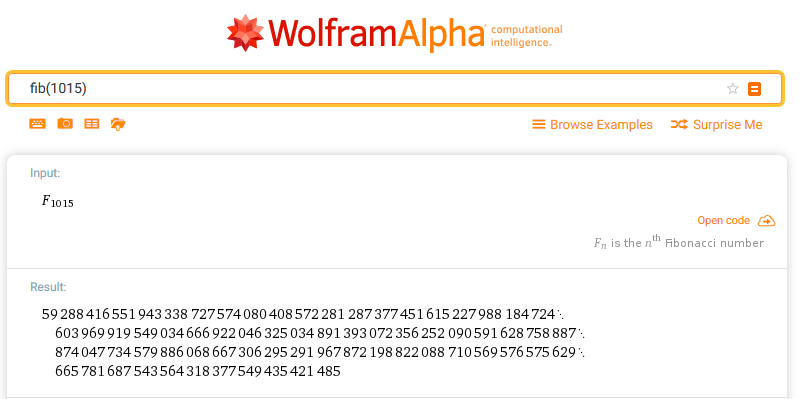
fib(1015) = 59288416551943338727574080408572281287377451615227988184724603969919549034666922046325034891393072356252090591628758887874047734579886068667306295291967872198822088710569576575629665781687543564318377549435421485

At this point, the result would be stored into eax which is a 32-bit register, an int (in my architecture at least) is 32 bit too, so in order to quickly have the right number and ignore the overflow, I just put that result in an int variable, and make it print.

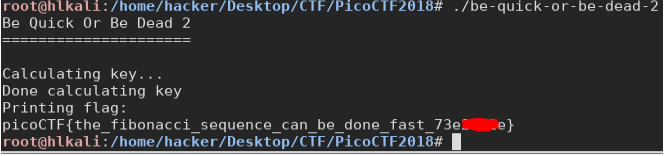
now we just want to patch the

“call fib” with “mov EAX, 3611214637”

and we win.

be-quick-or-be-dead-3

Here we have again the same challenge, whit again a 3s timer, and a calculate_key too time-demanding. But this time, the function which calculates the key isn’t fib(), but a generic calc(). We need to reverse it.

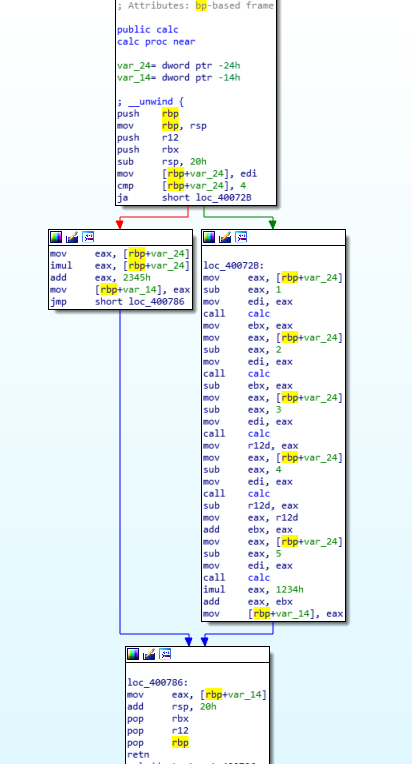
Luckily it is quite simple:

in short, it does:

unsigned int calc(unsigned int x)
{
    unsigned int v1; 
    unsigned int v2; 
    unsigned int v3; 
    unsigned int v4; 
    unsigned int v5; 

    if ( a1 > 4 )
    {
        v1 = calc(x - 1);
        v2 = v1 - calc(x - 2);
        v3 = calc(x - 3);
        v4 = v3 - calc(x - 4) + v2;
        v5 = v4 + 4660 * calc(x - 5);
    }
    else
    {
        v5 = x * x + 9029;
    }
    return v5;
}

okay, again an exponential-recursive funciton, which has as input 19965h.

no way it can’t be solved in this way.

We just need to rewrite it in a linear-complexity. (dynamic programming if you want):

This was my implementation:

#define N 104806
unsigned int v[N]={0};
int main() {

    int i;
    unsigned int v1,v2,v3,v4;
    v[0]=9029;
    v[1]=9030;
    v[2]=9033;
    v[3]=9038;
    v[4]=9045;
    for(i=5;i<N;i++){
        v1=v[i-1];
        v2=v1-v[i-2];
        v3=v[i-3];
        v4=v3-v[i-4]+v2;
        v[i]=v4+4660*v[i-5];
    }
    printf("%u",v[N-1]);
    return 0;

we take the result, keep only the lowers 16 bits, patch the program with: “MOV EAX,9E22C98Eh” as in be-quick-or-be-dead-2, and run it.

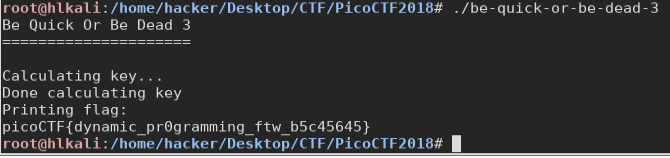
and that’s it. We solved all those 3 challenges, they were simple and nice!

XxcoralloxX